Задачи по спросу и предложению — налоги и дотации
Задачи для самостоятельного решения
(внимание: ответы под спойлером; не открывайте решение, пока не решите задачу).
Задача 1
Предложение на рынке товара выражается формулой Q=0,5P+2 а спрос — формулой Q=8-P.
Государство ввело налог на производителей в размере 3 денежных единицы на каждую единицу продукции. На сколько процентов возрастет равновесная цена?
Решение графическое
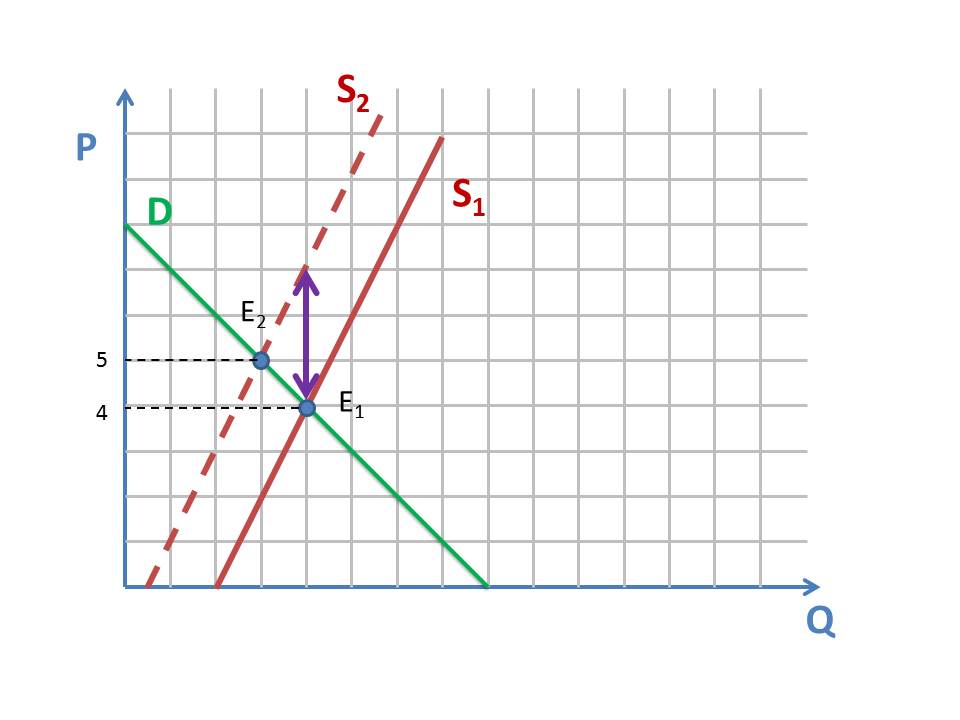
При введении налога в 3 денежных единицы на 1 единицу продукции кривая предложения переместится на 3 денежных единицы вверх, из S1 в S2, а поскольку спрос останется старым, точка равновесия переместится из Е1 в Е2. Равновесная цена вместо 4 станет 5, то есть увеличится на 25%.
Решение (алгебраическое — сложное, на любителя, я бы так не решал)
Нетрудно найти равновесную цену до введения налога. Нужно просто приравнять спрос и предложение:
0,5P+2=8-P
Отсюда получим P=4
Теперь найдем новую равновесную цену. Для этого нужно рассчитать новую кривую предложения. Это можно сделать двумя способами
Первый способ
Вначале переведем функцию предложения
Q=0,5P+2
в обратную функцию предложения (то есть выразим P через Q).
P=2Q-4
Цена будет больше исходной на 3 денежных единицы, следовательно, к ней нужно прибавить 3
P=2Q-4+3
то есть
P=2Q-1
Переводим обратную формулу назад в обычную формулу предложения (выражаем Q через P)
Q=0,5P+0,5
Второй способ
Новая цена P2 будет больше начальной Р2 на 3. То есть
P2=P1+3
или
P1=P2-3
Подставляем правую часть в начальную формулу предложения
Q=0,5(P2-3) +2
Откуда получаем
Q=0,5P2+0,5
Это новая формула предложения. Формула спроса осталась прежней. Приравняем их
0,5P+0,5=8-P
Отсюда
P=5
Таким образом, равновесная цена P вместо 4 стала 5, то есть выросла на 5/4-1=0,25 или 25%.
Задача 2
Предложение на рынке товара выражается формулой Q=2P-4 а спрос — формулой Q=12-2P.
Государство решило ввести потоварный налог на производителя, чтобы сократить потребление этого товара (который государство считает вредным) вдвое.
Какого размера налог нужно ввести государству?
Решение (графическое)
Построив график, можно увидеть, что равновесное количество равно 4 (например, тысяч тонн)
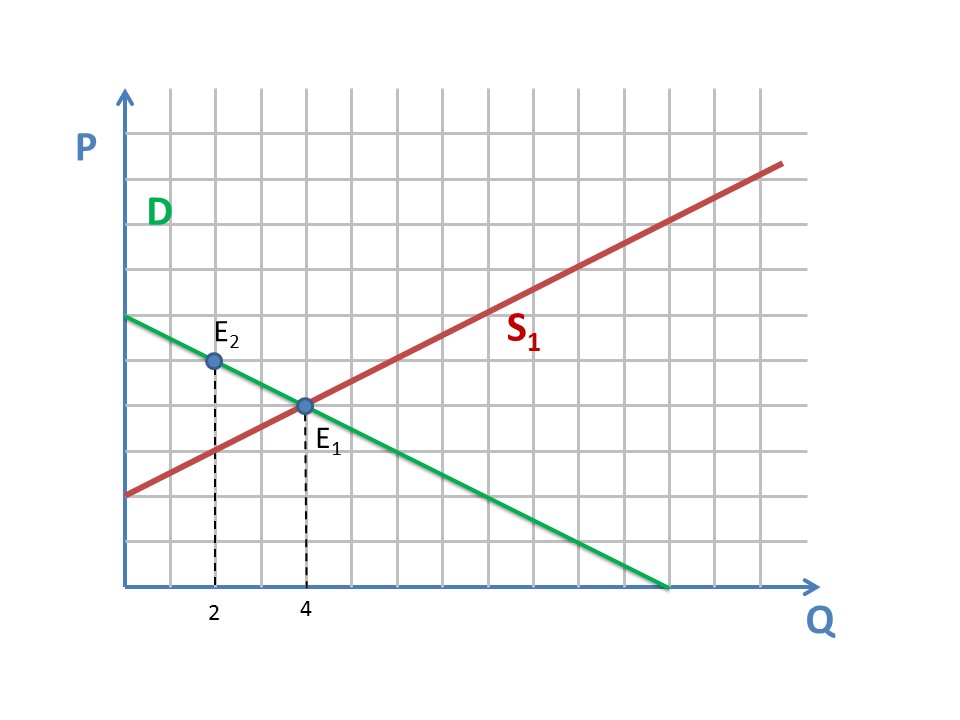
Очевидно, что государство хочет, чтобы равновесное количество равнялось 2 (тысячам тонн).
Поскольку на спрос налог никак не воздействует (то есть кривая спроса останется той же), очевидно, что точка равновесия должна переместиться в Е2.
Необходимо провести новую кривую предложения S2, параллельную кривой предложения S1 и проходящую через Е2.
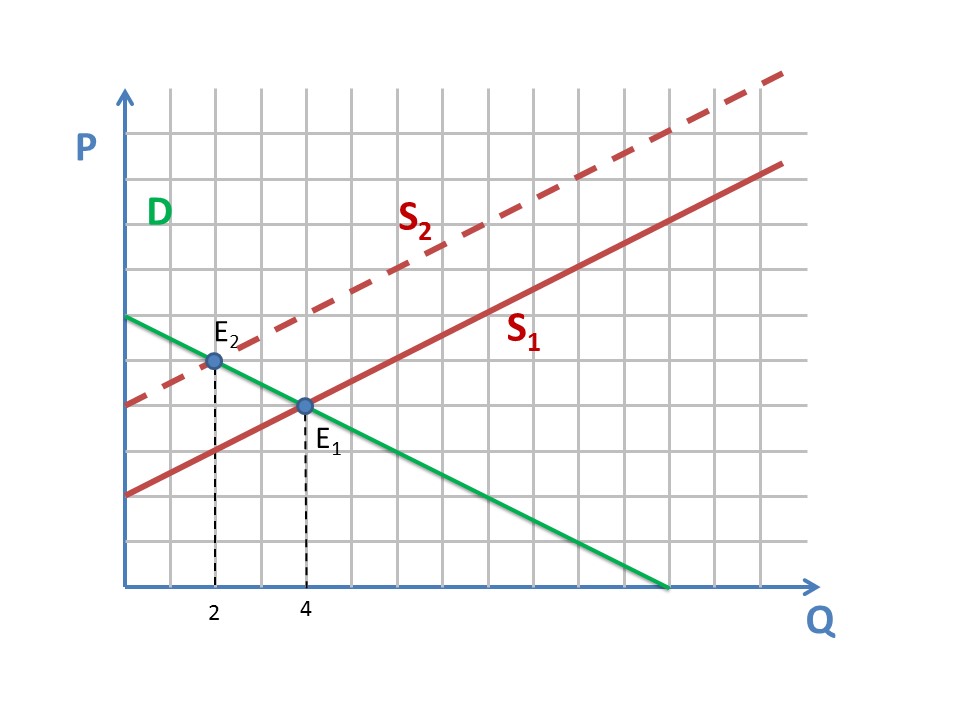
Можно увидеть, что она лежит на 2 деления выше линии S1.
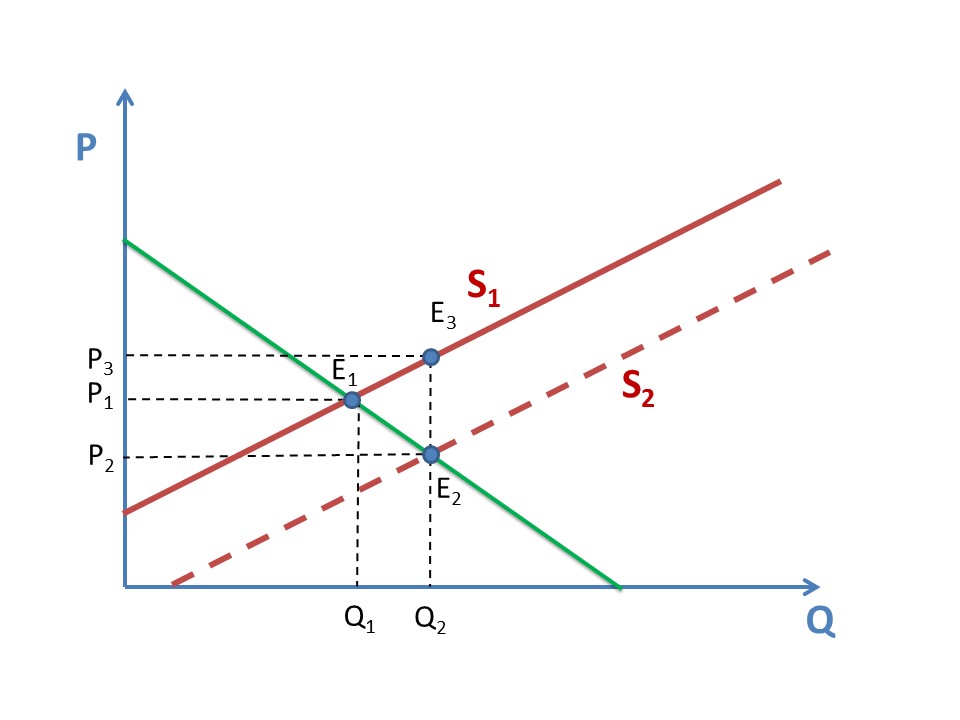
На самом деле, можно даже не проводить кривую, а просто измерить расстояние между Е2 и Е3 на следующей диаграмме:
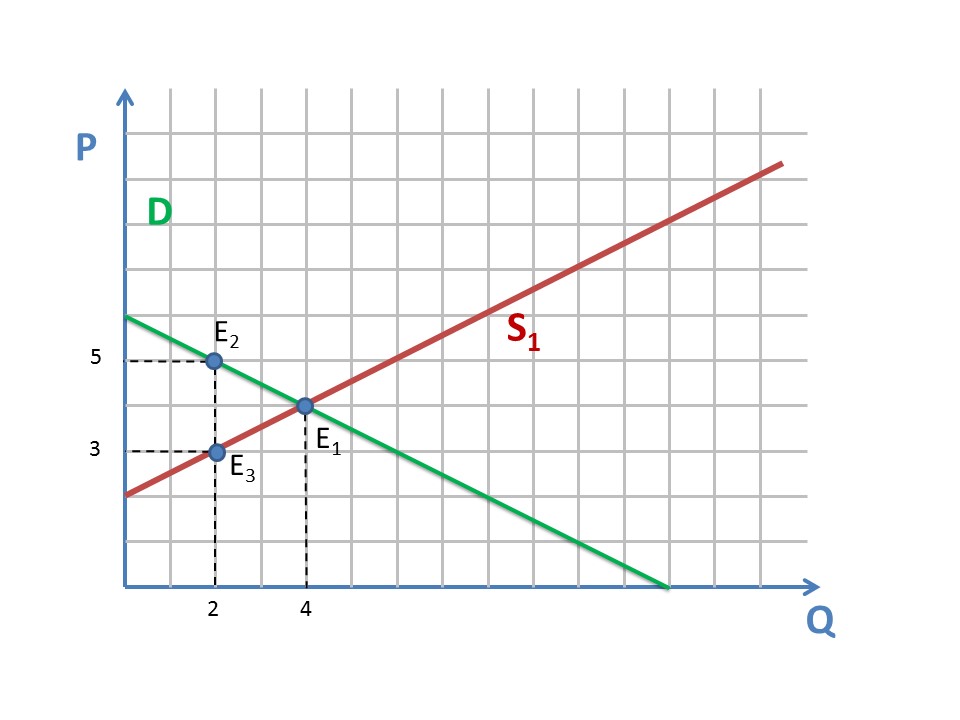
Точка Е3 обозначает предложение в размере 2 тысячи тонн при старой кривой предложения S1, а точка Е2 — предложение того же размера при новой кривой предложения S2. Разницу между ними легко посчитать, что и является основой алгебраического решения.
Разумеется, разница равна 2 денежных единицы, что и является размером налога.
Решение (алгебраическое — простое, если вы уже рассмотрели графическое)
Это решение хорошо в том случае, когда кривые сложные, пересекаются не видно где. Нарисуйте набросок вроде того, что приведен в предыдущем решении, и считайте.
Первый шаг: определяем равновесную цену. Просто приравниваем спрос и предложение
2P-4=12-2P
Из чего получаем
P=4
Теперь определяем равновесный объем. Для этого подставляем только что полученное значение Р в формулу спроса или предложения — это безразлично, они через одну точку проходят. Получаем:
Q1=4
Теперь понятно, что государство хочет довести объем до
Q2=4/2=2
Этот новый объем Q2подставляем в форму спроса:
Q2=12-2P
2=12-2P
P2=5
Это цена для точки Е2, то есть равновесная цена после введения налога.
Подставляем Q2 в формулу предложения:
Q2=2P-4
2=2P-4
P3=3
В результате получаем:
P2—P3=2
Теперь вы сможете решить следующую задачу, в которой графический метод вам нужен только для наброска.
Задача 3
Эту задачу решить непросто, не разобрав предыдущую.
Спрос на рынке молока равен Q=7-5/7*P , а предложение равно Q=3/7*P+2.
Государство хотело бы ввести такую потоварную дотацию для производителей молока, чтобы его цена для покупателей снизилась на 20%. Какого размера дотацию оно должно ввести? На сколько процентов возрастут покупки молока?
Графически (по клеточкам) эту задачу не решить — ответы будут в бесконечных десятичных дробях.
Решение (алгебраическое)
Будет понятнее, если вы сделаете набросок вроде этого.
Равновесие до введения дотации находится в точке Е1. Прежде всего, определим исходную равновесную цену P1, просто приравняв спрос и предложение.
7-5/7*P=3/7*P+2
Откуда
P1=35/8
Государство хотело бы довести цену до P2, которая, по условию, на 20% ниже.
P2=P1*80%=35/8*80/100=7/2
При такой цене спрос будет равен (точка Е2)
Q2=7-5/7*P2=7-5/7*7/2=9/2
Однако предложение для такого количества, если не ввести дотацию (по старой кривой предложения S1) для такого количества будет находиться в точке Е3. Посчитаем, по какой цене производитель готов предоставить данное количество товара. Для этого приравняем формулу предложения к рассчитанному Q2.
3/7P+2=Q2
3/7P+2=9/2
P3=35/6
Значит, чтобы сдвинуть кривую предложения вниз, нужно ввести дотацию в размере
P3—P2=35/6-7/2=7/3
Это и есть первый ответ: 7/3
Теперь посчитаем, насколько увеличатся продажи молока. Очевидно, они из Q1 перейдут в Q2.
Q1 рассчитать просто, достаточно Р1 подставить в исходную формулу спроса или предложения — безразлично. Ну, например, спроса:
Q1=7-5/7* Р1 =7-5/7*35/8=31/8
А Q2 мы уже рассчитывали выше, он равен 9/2
Таким образом, Q2 относится к Q1 как
Q2/Q1=9/2:31/8=36/8:31/8=36/31
То есть Q2 больше Q1 на
36/31-1=5/31
Вот и второй ответ: молока будут покупать больше на 5/31, то есть примерно на 16%.


