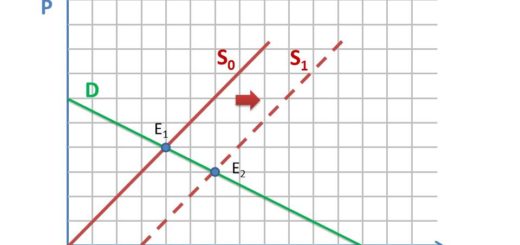
Разбор контрольной от 23 ноября
Про спрос, предложение, налоги, дотации, эластичность и т.п.
Задача 1
Кривая предложения имеет формулу Q=P-9, а спроса Q=12-0,5P. Государство хотело бы увеличить покупки (а значит, потребление) этого полезного продукта на 20% путем предоставления потоварных дотаций производителям.
- Какова сейчас равновесная цена: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]14[/spoiler]
- Какую дотацию на один товар нужно ввести государству: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’] 3 [/spoiler]
- Какова будет тогда равновесная цена: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’] 12 [/spoiler]
- Как при этом изменится излишек потребителя:
(тут и дальше ответ приводите в форме: «уменьшится (увеличится) на столько-то д.е.») [spoiler title=’ответ’ style=’purple’ collapse_link=’true’] увеличится на 11[/spoiler] - А как изменится излишек производителя: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]увеличится на 5,5 [/spoiler]
- Какую сумму дотаций выплатит государство: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]18 [/spoiler]
- Каковы будут чистые потери общества: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]1,5 [/spoiler]
[spoiler title=’Решение’ style=’brown’ collapse_link=’true’]
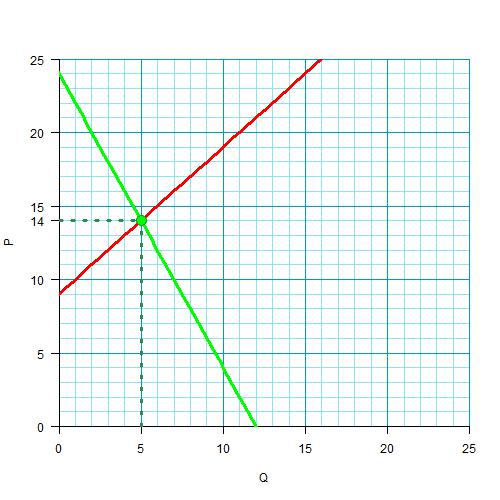
Рисуем кривые и находим равновесную цену и количество: 14 и 5
Также можем посчитать излишки производителя и потребителя — они заштрихованы на этой картинке:
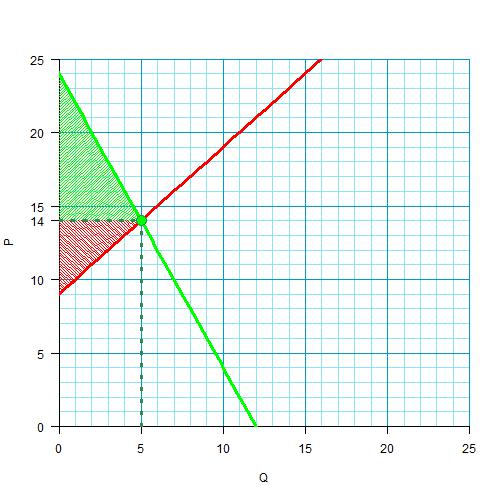
Соответственно 25 и 12,5.
Если государство хочет увеличить потребление на 20%, значит, оно хочет довести его до 5+20%*5=5+1=6. Дотации производителю меняют кривую предложения, а кривая спроса останется той же. Значит, новая точка равновесия будет на кривой спроса, там, где количество равно 6:
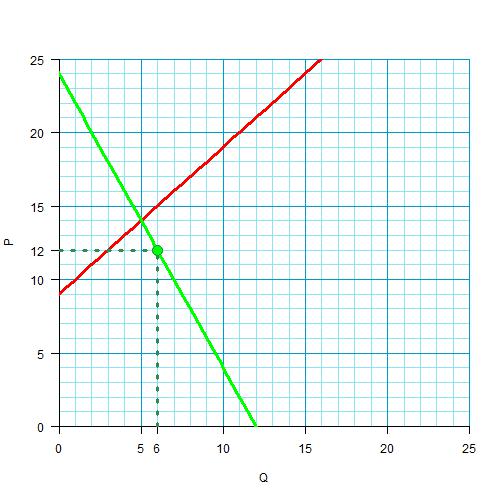
Кривая предложения переместится вниз на размер дотации. Поскольку старая линия предложения — это прямая, то и новая линия предложения будет прямая, параллельная старой. И она должна пройти через новую точку равновесия. Нарисуем эту новую линию.
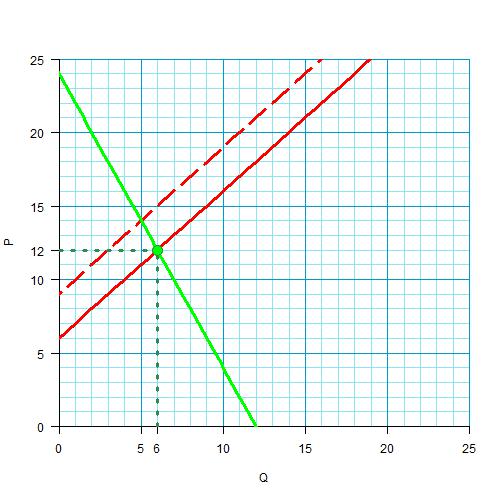
Размер дотации — это то, насколько сдвинулась линия вдоль оси цены.
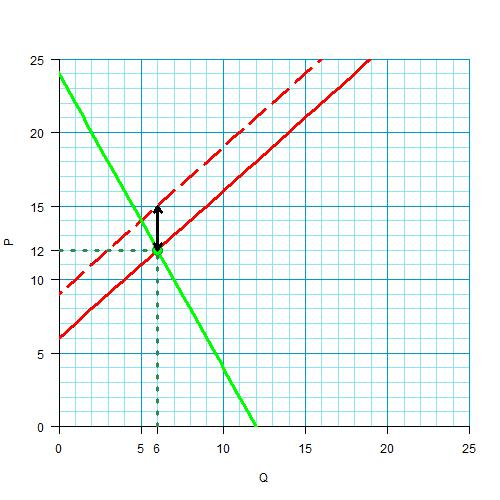
Для любой точки на кривой предложения это расстояние одинаковое. Так, раньше производитель готов был предложить 6 единиц по цене 15, а теперь то же количество предложит по цене 12. Значит, 3 денежных единицы ему доплачивает государство. 3 — это и есть размер дотации.
Теперь посчитаем новые излишки производителя и потребителя:
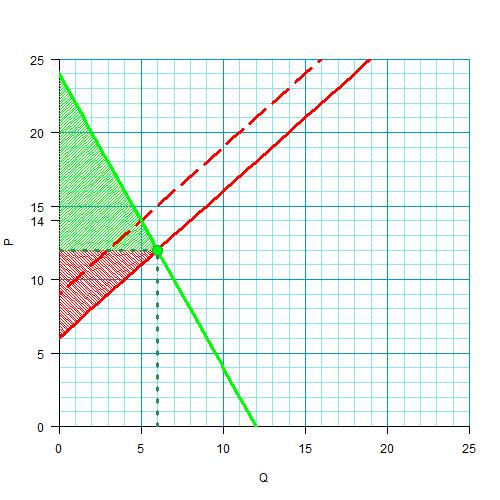
Видим, что они равны, соответственно 36 и 18.
Собственно, дальше можно просто все посчитать. Излишки производителя возросли на 11, покупателя — на 5,5. Дотаций государство заплатит 6*3=18 (6 — это сколько товаров будет продаваться после введения дотации — см. график, а 3 — это размер дотации на каждый товар). А излишки всего выросли на 16,5. Значит, 1,5 куда-то потерялось. Это и есть чистые потери общества.
Ну а если хочется графической интерпретации — то вот, пожалуйста. Сместим излишки покупателя к старой кривой предложения. Они перекрываются с излишками продавца:
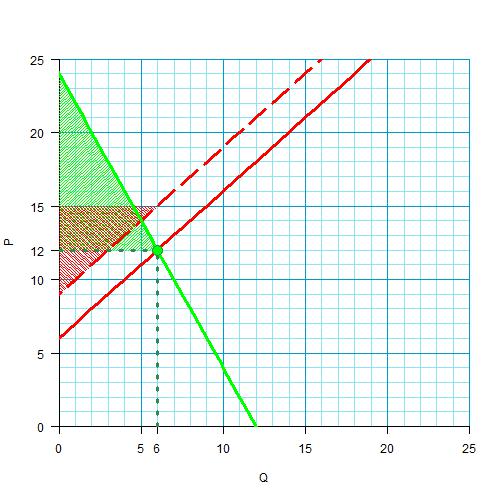
Зато теперь, сравнив эту картинку с картинкой излишков до введения дотации, можно легко увидеть, насколько изменились излишки. Вот настолько (они уже не перекрываются):
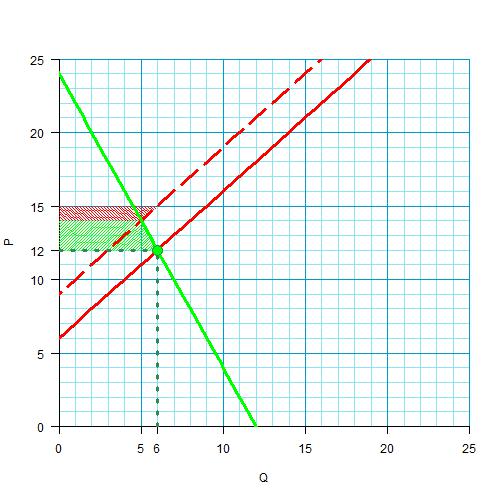
А дотаций государство платит вот столько:
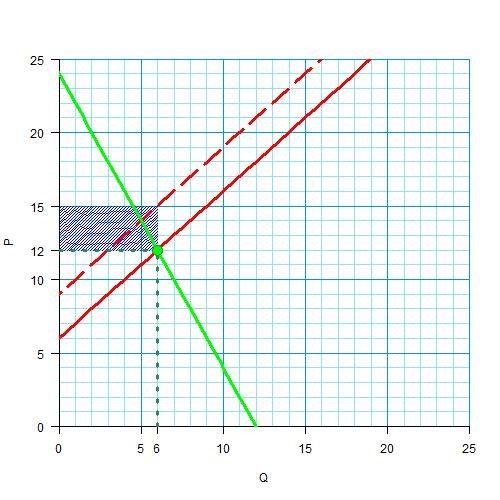
Значит, оставшийся треугольничек — это чистые потери общества
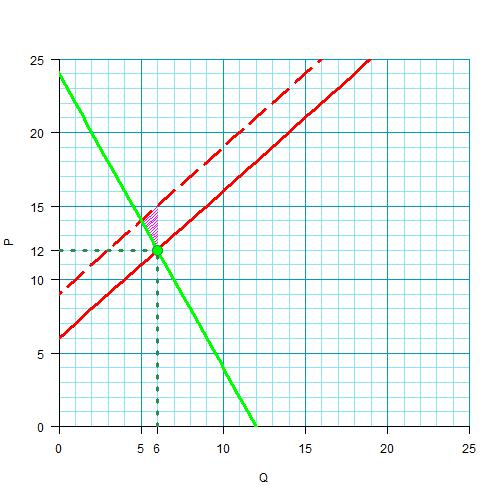
Основание его — 3, а высота — 1 (поверните голову на 90 градусов влево). Площадь — 1,5.
[/spoiler]
Задача 2
Кривая предложения имеет формулу Q=3P, а спроса Q=9-1.5P. Государство хотело бы снизить потребление этого неполезного продукта в два раза. Это можно сделать либо установлением обязательной минимальной цены, либо введением потоварного налога.
- А. Если государство выберет вариант введения минимальной
цены, то какую цену оно должно установить: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]4[/spoiler]- Как при этом изменятся излишки потребителя: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]уменьшатся на 9 [/spoiler]
- А как изменятся излишки производителя: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]увеличатся на 4,5 [/spoiler]
- Каковы будут чистые потери общества: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]4,5[/spoiler]
- Б. Если государство выберет потоварный налог, то каков должен быть его размер: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]3 [/spoiler]
- Как при этом изменятся излишки потребителя: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]уменьшатся на 9[/spoiler]
- А как изменятся излишки производителя: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]уменьшатся на 4,5 [/spoiler]
- Сколько всего налогов получит государство: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]9[/spoiler]
- Каковы будут чистые потери общества: [spoiler title=’ответ’ style=’purple’ collapse_link=’true’]4,5[/spoiler]
[spoiler title=’Решение’ style=’brown’ collapse_link=’true’]
Сначала, как обычно, рисуем начальные кривые и находим равновесную цену и количество, а также излишки:
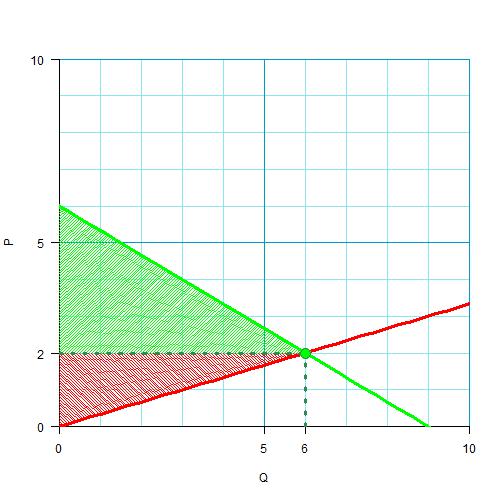
Поскольку количество равно 6, то понимаем, что государство хочет снизить его до 3 — это и будет в два раза. Как его можно снизить? Очевидно, установив такую цену, чтобы покупатель смог купить только 3 единицы. Логично, что это можно сделать, либо запретив продавать дешевле на законодательном уровне (да, иногда делают именно так), либо введя дополнительные налоги на производителя, что заставит его продавать товары дороже. Вначале найдем эту новую цену, это несложно, это точка на кривой спроса, соответствующая количеству 3:
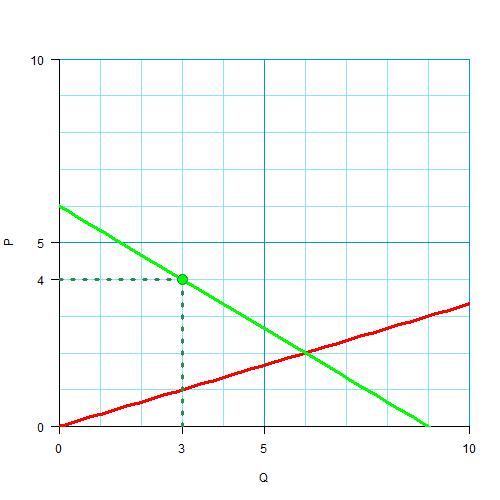
Значит, если государство запретит продавать товар ниже 4 ден. единиц, то его как раз и купят в два раза меньше.
А вот дальше многие из вас высчитали излишки неверно! Вот так:
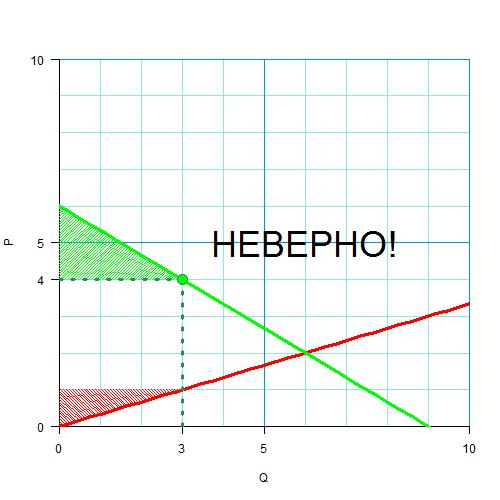
Нет, конечно! Производитель продает за 4 единицы тот товар, который он готов был продать за 1 единицу. Вся разница — это его излишек! Вот как:
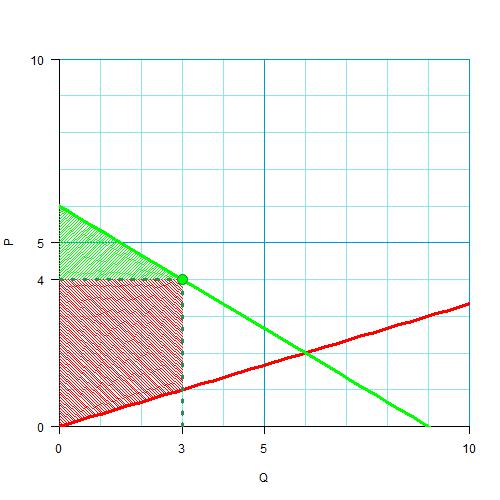
Излишек производителя в случае повышенной цены может даже возрасти, как в нашем случае (вообще это зависит от наклона кривой предложения).
Сравните с первой картинкой и убедитесь, что общая сумма излишков производителя и потребителя снизилась вот на этот треугольник, который и есть чистые потери общества.
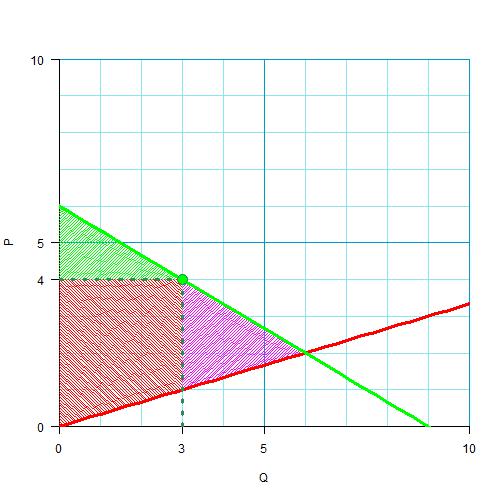
Случай с налогом, думаю, вам понятен. Вообще все будет почти так же, как на предыдущем рисунке: в частности, излишек потребителя будет ровно тем же (для покупателя вообще никакой разницы, как образовалась цена в 4 единицы), и чистые потери общества будут те же. А вот излишек производителя будет другим, ведь он, получив от покупателя 4 денежных единицы, должен будет 3 из них отдать в качестве налога:
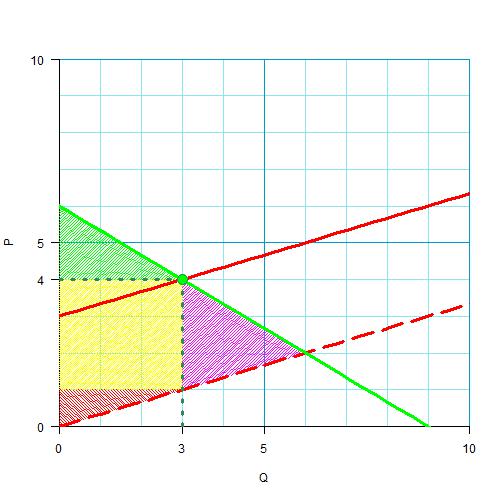
Вот эта желтая область и будет размером налогов, полученным государством: количество товаров умноженное на размер налога на один товар.
Вы видите, что случаи с минимальной ценой и налогом практически одинаковые. Отличие в том, что та сумма, которую государство может получить в качестве налога, становится при установлении минимальной цены излишком производителя, а государство ничего не получает.
— Постойте! — скажете вы. — Почему же тогда наше государство устанавливает минимальную цену на водку, вместо того, чтобы ввести налоги на ее производителей? Зачем оно добровольно отдает деньги производителям алкоголя? Нет ли тут сговора?
Ответ на этот вопрос вы найдете в следующем спойлере
[/spoiler]
[spoiler title=’Ответ на вопрос, который содержится в конце предыдущего спойлера, и который лучше увидеть после того, как вы прочтете вопрос’ style=’brown’ collapse_link=’true’]
Потому что все не так просто.
Если бы государство ввело налог на производителей водки, вместо того, чтобы устанавливать минимальную цену, то у производителей был бы стимул не повышать цену на алкоголь, а снизить себестоимость, ухудшив его качество. На рынок хлынули бы суррогаты и контрафакт, способные привести к тяжелым последствиям: отравлениям, слепоте и даже летальному исходу. А если цена одинаково высока, то создается избыточное предложение, производителям приходится прибегать к неценовым методам конкуренции, в том числе улучшению качества.
Это связано с особенностями продукта: речь идет о потенциально опасном товаре. Если бы государство хотело, например, ограничить потребление меховых изделий, чтобы защитить пушных зверей от избыточного промысла, то введение налога было бы вполне оправдано: возможное ухудшение качества меха не угрожает здоровью граждан.
[/spoiler]
Задача 3
Формула предложения Q=3P-2. Известно, что формула спроса носит линейный характер, равновесная цена равна 2, причем в точке равновесия спрос имеет эластичность -0,75. Какова формула спроса?
[spoiler title=’Ответ’ style=’purple’ collapse_link=’true’]Q=7-1,5P[/spoiler]
[spoiler title=’Решение’ style=’brown’ collapse_link=’true’]
Если формула спроса предложения линейная, то она имеет формулу
[latexpage]
$Q=aP+b$
где $a$ и $b$ — некоторые коэффициенты
А эластичность, как известно, имеет формулу:
$\frac{\Delta Q}{\Delta P}*\frac{P}{Q}$
При этом $\frac{\Delta Q}{\Delta P}$ — это наклон кривой в данной точке, или же производная.
Восстановить формулу кривой по точке и эластичности просто, нужно через эту точку провести линию, имеющую соответственный наклон.
Графически это делается так:
Сперва находим нужную точку.
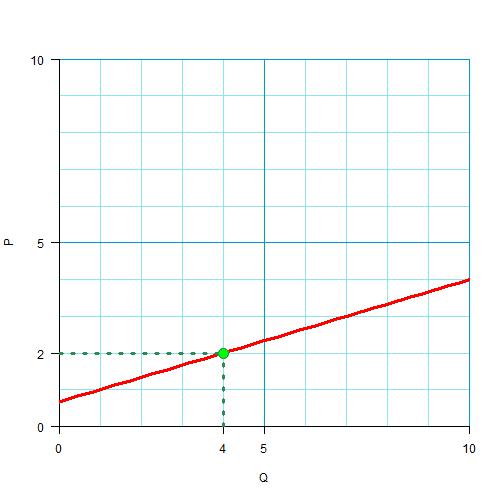
Видим, что это Р=2, Q=4. Мы также знаем, что эластичность в этой точке равна 0,75
$\frac{\Delta Q}{\Delta P}*\frac{P}{Q}=0,75$
Подставляем значения P и Q:
$\frac{\Delta Q}{\Delta P}*\frac{2}{4}=-0,75$
$\frac{\Delta Q}{\Delta P}=-1,5$
Теперь мы знаем, что наклон кривой в этой точке 1,5, то есть при изменении P на 1 единицу (${\Delta P}=1$) Q должно измениться на 1,5 (${\Delta P}=-1,5$)
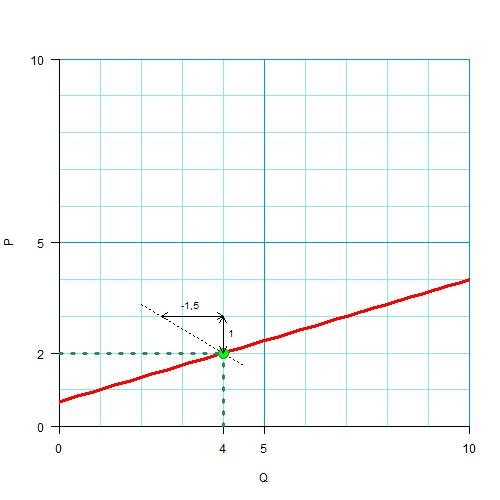
Касательная к прямой — это сама прямая, и мы можем ее нарисовать.
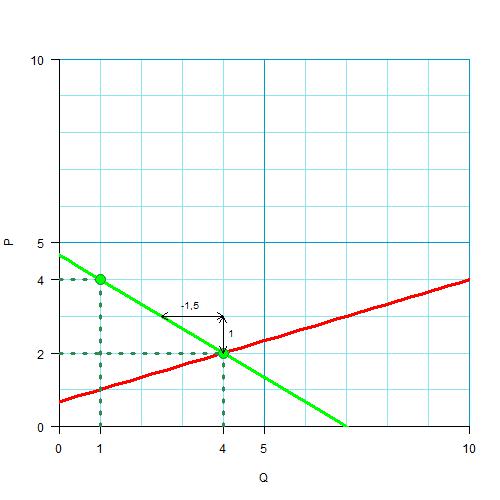
А дальше восстановить формулу, например, по двум точкам, подставив их значения в формулу $Q=aP+b$:
$\left\{\begin{matrix}
1=a4+b
\\
4=a2+b
\end{matrix}\right$
Вычитаем второе из первого, получаем
$-3=a2$
значит
$a=-1,5$
$b=7$
Формула спроса — $Q=-1,5P+7$ или $Q=7-1,5P$
Алгебраически все даже проще:
Находим точку равновесия, подставив P=2 в формулу предожения
$Q=3P-2=3*2-2=4$
Теперь точно так же, как в предыдущем случае подставляем P и Q в формулу эластичности, помня, что она равна -0,75
$\frac{\Delta Q}{\Delta P}*\frac{P}{Q}=0,75$
$\frac{\Delta Q}{\Delta P}*\frac{2}{4}=-0,75$
$\frac{\Delta Q}{\Delta P}=-1,5$
Вспоминаем, что $\frac{\Delta Q}{\Delta P}$ — это производная в данной точке. А производная функции $aх+b$ равна просто $a$.
Теперь мы знаем коэффициент $a$ функции спроса: $a=-1,5$
$Q=-1,5P+b$
Подставляем значения известной нам точки
$4=-1,5*2+b$
Получаем
$b=7$
Теперь у нас есть оба коэффициента линейной функции. Значит, она выглядит так
$Q=-1,5P+7$ или $Q=7-1,5P$
[/spoiler]
Задача 4
Известны две точки кривой спроса: P1=3, Q1=3 и P2=2, Q2=6.
A. Какова дуговая эластичность на отрезке между этими точками: [spoiler title=’Ответ’ style=’purple’ collapse_link=’true’]$1\frac{2}{3}$[/spoiler]
Б. Если функция спроса носит линейный характер, какова точечная эластичность в точке P1: [spoiler title=’Ответ’ style=’purple’ collapse_link=’true’]-3[/spoiler]
[spoiler title=’Решение’ style=’brown’ collapse_link=’true’]
А. Формула дуговой эластичности:
$e=\frac{Q_{2}-Q_{1}}{P_{2}-P_{1}}*\frac{P_{2}+P_{1}}{Q_{2}+Q_{1}}$
Подставляем значения
$e=\frac{6-3}{2-3}*\frac{2+3}{6+3}$
$e=\frac{3}{-1}*\frac{5}{9}$
$e=\frac{3*5}{-1*9}$
$e= -\frac{5}{3}= -1\frac{2}{3} $
Б. Сначала восстановим кривую спроса по двум точкам, помня, что формула линейной зависимости — $Q=aP+b$, где $a$ и $b$ — некоторые коэффициенты. Подставим известные нам значения $P$ и $Q$, получив систему уравнений
$\left\{\begin{matrix}
3=a3+b
\\
6=a2+b
\end{matrix}\right$
Вычитаем второе из первого, получаем
$-3=a$
тогда
$b=12$
А формула спроса:
$Q=-3P+12$
Формула эластичности:
$e=\frac{\Delta Q}{\Delta P}*\frac{P}{Q}$
При этом $\frac{\Delta Q}{\Delta P}$ — это эластичность формулы спроса. По формуле спроса ее легко вычислить:
$Q’=-3$
Значит
$e=-3*\frac{P}{Q}$
Подставляем значения P и Q для искомой точки
$e=-3*\frac{3}{3}$
$e=-3$
[/spoiler]